GASで何らかのWebhook通知を受け取ってログに書き出すまで
Scrapbox の Slack 通知の中身を調べたかったので、GAS で受け取ってログに吐いてみることにした。
GAS 触るのは初めてだったので色々ハマったり色々調べたりした。以下、分かったこととかをつらつらと。
GAS の種類
Sheets や Docs に紐付いてるパターン(コンテナバウンド)とそうでないパターン(スタンドアローン)がある。
"Google Apps Script" でググって出てきたページから流れで作っていくとスタンドアローンタイプになる。
紐付いてるやつ作りたかったらまず Sheet とかを作って、そこからスクリプトを作成するという手順を踏む必要がある。
特に Sheet は DB みたいに使えるのでよく使いそう。*1
GCP プロジェクト
1 つの GAS には 1 つの GCP(Google Cloud Platform) プロジェクトが必ず紐付いてるもんらしい。
何も考えず作ってると、自動で作られた「デフォルト GCP プロジェクト」に自動で紐付いてる状態になる。
しかしこの状態では使えない機能がいくつかある。それらを使いたければ「スタンダード GCP プロジェクト」に紐付ける必要がある。
「スタンダード GCP プロジェクト」は、GAS ではなく GCP のページを開いて、そこで自分で作ったプロジェクトのことを指すっぽい。
これを作ったら後は GAS 側の設定画面で GCP プロジェクト ID を指定すれば紐付けできる。
……と思いきや、「OAuth 同意画面を設定する必要があります」と怒られて紐付けに失敗してしまった。
仕方ないので、GCP プロジェクトの設定画面から「OAuth 同意画面」という項目を見つけ、よしなに設定していく。
User Type は「内部」と「外部」があるが、「Google Workspace ユーザーではない」とか言われて「内部」は選べなかった。
正直意味を何も理解してないので、選択肢が勝手に限られてくれるのはありがたい。
他の設定項目もよくわからないので全部テキトーに設定したが、これで GAS に紐付けることができるようになり、Cloud Logging 機能(後述)が無事使えるようになった。
どうやら設定した内容は今回使いたい機能(Cloud Logging)と関係無かったっぽい。
なんでこの作業必須なんだろう。
デプロイの種類
スクリプトをデプロイしようとすると、
- ウェブアプリ
- 実行可能 API
- アドオン
- ライブラリ
の4つの中からデプロイの種類を選べと言われる。
ウェブアプリは doGet(e) や doPost(e) という関数を定義しておく必要があるやつ。
それぞれ GET 時や POST 時に実行される。
ちなみにこれらの関数は HTMLOutput や TextOutput オブジェクトをリターンする必要がある。(ContentService を使う。)
ライブラリは他のプロジェクトで使うための関数群。
ちなみにライブラリを取り込む際にはスクリプト ID を指定する形式となる。ライブラリを検索できるプラットフォームとかは特にないっぽい。
ちなみにちなみに、ライブラリは取り込むと実行が遅くなってしまうらしい。公式ガイドにわざわざ警告文が書いてあった。あんま使わないほうが良さそう。
公式ガイドから読み取れたのはここまで。
実行可能 API もアドオンも特に説明が見つからない。
なんでなんだ。
実行可能 API が一番わかんない。ウェブアプリとどう違うのか。あと実行不可能な API も果たしてあるのか。
まあ多分だけど、実行可能 API だと doGet(e) とか doPost(e) を動かす感じではなく、トップレベルの関数を名前指定して実行する感じになるっぽい。
アドオンは多分 GMail とか Google Calendar とかでインストールできるやつ。
アドオンストアに登録することになるっぽい。
実行可能 API とアドオンは、前述の「スタンダード GCP プロジェクトへの紐付け」が必要なようだった。
とりあえず今回の「Webhook 通知を受け取ってログに書き出す」という目的に対してはウェブアプリで良さそう。
エディタ画面
デフォルトではコード.gsという 1 ファイルのみがあるが、複数ファイルあっても良いらしい。
デフォルトでは appsscript.json というマニフェストファイルが非表示になっている。
設定で表示させることも可能。
依存ライブラリとかはここで管理されてるっぽい。
まあ自動で管理されてるし、あんま自分で触る必要は無さそう。
エディタにはコードのリストの他に、取り込んでるライブラリのリストとサービスのリストが表示されている。
ライブラリは前述の通り。
サービスは多分 Google が用意してくれてるやつで、他サービスの API 叩くためのやつが多そう。
エディタ画面でコードを書いたらちゃんと保存する必要がある。
ブラウザ上のエディタって自動保存されるパターンが多いので、この仕様に気付くまでかなり時間かかったし、知った今でも油断すると忘れる。
せめてデプロイ時ぐらいは自動保存とか、あるいは「保存されていないコードをデプロイしようとしています。よろしいですか?」って警告ぐらいはしてほしい。
ちなみに command + S みたいなショートカットは使える。
ロガー
ログ出力には console と Logger の 2 種類がある。
特に出力先とかが変わるわけではなさそう。
undefined を渡した時に後者は null って出力してきた。怪しげ。
console には log, info, warn, error とかがある。
console.log の severity は DEBUG。
一方で Logger にあるログ出力関数は log のみで、severity は INFO。
かわりに Logger の方には getLog とかがある。
console の方は GAS じゃない JavaScript とも互換性ありそうだし、こっちの方が良さそう。
コード
function doPost(e) { console.info('post data type:', e.postData.type); console.info('post data:', e.postData.contents); var output = ContentService.createTextOutput('received POST'); return output; }
とりあえずこれで動いたしログも見れた。
postData.type は MIME のこと。
追記:const 使ってよかったらしい。
現在のGoogle Apps Scriptはアロー関数やlet, constが使用可能に | iwb.jp
デプロイ設定
デプロイの種類「ウェブアプリ」を指定したら、具体的な設定をいくつか求められる。
「次のユーザーとして実行」については「自分」か「ウェブアプリケーションにアクセスしているユーザー」を選べる。
後者だと Google アカウント持ってる人がブラウザで叩かないと動かない気がする。
「アクセスできるユーザー」については「自分のみ」か「Google アカウントをもつ全員」か「全員」を選べる。
今回はやはり「全員」じゃないとダメそう。
「説明」はデプロイバージョンのタイトルに使用されてるので、変更内容についての説明が求められてる気がする。
変更があれば都度、「新しいデプロイ」を選んでデプロイし直す。
URL は変わらない。
「デプロイを管理」で過去のデプロイ履歴が見れる。
「デプロイを管理」で最新のデプロイ設定を変更できるが、変更して「デプロイ」を押しても全く反映されなかった。もちろん設定だけじゃなく、コードの変更も反映されない。これ何のためにあるんだ。謎。
マルチアカウントで運用している際の罠
デプロイした URL にアクセスしてみると、「ファイルを開くことができません。」と表示された。
調べてみると原因は、「デフォルトの Google アカウント」でデプロイしなかったかららしい。
どうやら 1 番目にログインしたアカウントがデフォルトになるらしい。
デフォルトを変えるには他のアカウントをログアウトさせるしかないっぽい。
クソめんどくさい。
とりあえず GAS 書く時は普段使ってないブラウザを使い、1 アカウントだけでログインすることにした。
叩き方
curl の際には -L(--location)(Follow redirects)をつける必要がある。
ログを見る
ログには Apps Script execution log と Cloud Logging(と Error Reports)があるらしい。
前者はちょっとの間残る、後者は結構な日数残る、らしい。
また、後者は GCP プロジェクトで見るもののようで、前述の「スタンダード GCP プロジェクトへの紐付け」が必要になる。
出力の仕方はどちらも変わらず。前述のように Logger か console を使えば良い。
閲覧インターフェースが 2 種類あるって感じだろうか。
ちょっとした関数をエディタ上でデバッグ実行してみると、exectuion log の方でログを見ることができた。
しかし、実際にデプロイしたウェブアプリの doPost(e) 内で吐かせたログは、 execution log ではなぜだか見れなかった。
しょうがないので、スタンダード GCP プロジェクトへの紐づけを済ませ、Cloud Logging の方で確認したら見れた。
ローカル開発
「GAS のコードはクラウド上にあるから、git で管理したりとかできなくて嫌だな〜」とずっと思っていた。
しかしどうやら Apps Script API という口があって、ローカルで書いたコードもこの API を通してデプロイしたりできる様子。
んでもって、その辺をよしなにやってくれる clasp というコマンドツールがあるらしい。
次からはローカルで開発し、GitHub 上でちゃんとソースを管理しつつ、clasp でデプロイ、みたいな流れで書きたいなぁ。
おわり。
*1:データ保存に関しては Properties Service という機能もあってキー・バリュー式にデータを管理できる。この場合にどれぐらい永続してくれるかはよく分からない。
スニペット管理コマンドツールの構想
きっかけ
競プロでよく出てくるコード片を、私は 1 つのリポジトリにまとめている。
テストコードも書いたりして管理している。
コンテスト参加中はこのリポジトリを開いて、欲しいコードを探してコピペしてくる運用だ。
まあしかしこの運用は、競プロというタイムアタック競技においては致命的と言っていいほど、手間と時間がかかってしまう。
というわけで、コード片(=スニペット)を手軽に挿入するためのやり方を模索する。
"スニペット"機能を使うか否か
こういった時、他の人はどうしているか。
エディタの"スニペット"機能を活用しているパターンを多く聞く気がする。
キーワードを打ち込んで tab を押すだけで、設定しておいたコード片を挿入できるやつ。
プレースホルダーを設定された部分は書き換えることもできたりする。
私のリポジトリからコード片を吸い出し、上手いことエディタ(例えば VSCode)の"スニペット"設定に変換し、同期する。
そんなツールを作ることは簡単だろう。
というか、既存のツールでありそうな気もする。
ただし、設定はあくまでエディタ依存だ。
例えば複数エディタを使い分けたりするなら、どのエディタにも設定を同期しておかなければいけなかったりする。
私は個人的にそこが気に入らない。
あるいは、エディタとは独立したスニペット管理アプリを使うことも考える。
なんかそういうのがあるのは聞いたことがある。
でもなんか、そんな色んなツールに依存するのもだるい気がする。
もっとこう、コマンドラインから一発で挿入できればそれで良い気がする。
私が管理しようとしているコード片は基本的に Go で書かれているのだが、Go のエコシステムでは「ジェネレーターを使う(作る)」というパターンが割と一般的だ。
cf.
Generating code - The Go Blog
GoGenerateTools · golang/go Wiki · GitHub
メタプログラミングの発想をすることはちょくちょくあっても、メタプログラミング部分を実際のコードとは切り離した形で運用する、という発想は個人的には見落としがちなので、おもしろい。
Go の言語仕様は素朴で、Ruby みたいにメタプログラミング向けの言語機能が充実しているわけではない。だからこその文化なのだろうか。(まあしかし Ruby でも rails generate とかあったりするので、これまた興味深い。)
まあとにかく、コード片はコマンドラインで管理してみたい。
go generate を上手く活用する手もあるのかもしれない(よく分かってない)が、とりあえずは普通に標準出力にコード片を吐き出すだけのコマンドがあれば十分な気がする。
仮にコマンド(≒ツール名)を gnip としよう。(go と snippet から想起した造語。clip とも似ている。グニッって感じで音的にも気持ちいい。)
gnip sieveOfEratosthenes | pbcopy という感じでクリップボードに出力してしまえば、あとはペーストするだけでどこにでも挿入が可能だ。
案1. 探索パス内からコード片を探し出す
実装案の話。
最初に思いついたのは、「コマンド上で探索パスを登録できるようにする」という仕様だ。
前述の競プロ用リポジトリを gnip --register ~/Projects/src/github.com/ikngtty/go-contestlib/ という感じで登録しておく。
実際にやることとしては、テキトーな設定ファイル(~/.gnip みたいな)に保存しておく感じでいいだろう。
そんでいざ gnip sieveOfEratosthenes という感じでコード片を呼び出そうとした時には、探索パス上のコードファイルからキーワード(この場合 sieveOfEratosthenes)に当てはまるコード片を見つけ出して出力する。
「キーワードに当てはまる」とは具体的には、「関数名と一致する」で良いかなと思っている。
あるいは、コメントで
// gnip: start sieveOfEratosthenes func generatePrimes(max int) []int { return nil } // gnip: end sieveOfEratosthenes
みたいに指定するのも良さそうだ。
実装はこの方が楽だろう。
"スニペット"の管理ということで、やはりプレースホルダー機能も搭載したい。
Go は現在ジェネリクスが存在しないが、プレースホルダーを使えば任意の型についての型が量産できる。
例えば List<T> が作れない代わりに、{1:Int}List というスニペットから IntList や StringList がすぐに作れる。
interface{} のリストを作るよりは、個人的にはこの方が良さそうに思う。
interface{} のリストから値を取り出したら、わざわざ変換しないといけない。これは書く際にもコストだし、実行時間としてもコストになりそうな気がする。競プロにおいてはどちらも避けたい。
そんなわけでプレースホルダー機能は欲しい。
しかし、これは結構めんどくさいことに気づく。
// gnip: start list type anyList struct { headItem anyListItem tailItem anyListItem } type anyListItem struct { parent anyListItem value interface{} } // gnip: end list
は go のコードだ。実際に動かせるし、テストもできる。だが、
// gnip: start list
type @{1:int}List struct {
headItem @{1:int}ListItem
tailItem @{1:int}ListItem
}
type @{1:int}ListItem struct {
parent @{1:int}ListItem
value @{1:int}
}
// gnip: end list
みたいに独自の文法でプレースホルダーを導入しようとすると、これはもう go のコードではない。
強いて言えば .go.template のような拡張子になるだろう。
gnip --template list.go をすると list.go.template が自動で生成される。後は手動でプレースホルダーをメンテする。探索対象は拡張子が .template のファイルのみ。そんな感じ。
元コードに変更があった時の同期が大変そうだ。どうしよう。
一応
// gnip: start list any type anyList struct { headItem anyListItem tailItem anyListItem } type anyListItem struct { parent anyListItem value interface{} } // gnip: end list any
みたいにして、「gnip list int とすれば any が int に置換されますよ」みたいな仕様にもできる。
が、これは高確率で事故る。例えばコード辺の中に Many という単語が含まれていたら Mint になってしまったりする。
なのでさすがにこれはボツ。
そんなこんなでとにかく、プレースホルダー機能はめんどくさい。捨てた方がいいかもしれない。ジェネリクスもそのうち来るはずだし。
ところでこの .go.template ファイルであるが、どこに保存するの?という問題も残る。
よそのリポジトリにある .go ファイルの隣に勝手に .go.template ファイルを追加する。
追加された .go.template は、もちろん、そのリポジトリ上でコミットしておかないといけない。
これはちょっと嫌な感じ。
そもそも、// gnip: start とかいうコメントを入れるあたりから、そのリポジトリはもう gnip への依存が始まっている。
つまり、そのリポジトリは独立した意味をあまり持っておらず、gnip 配下のプロジェクトになっている。
こうなってくると、リポジトリを独立させて管理する意味があまりない気がする。
最初から gnip 専用のスペースでコード片を全部管理すればいいような気がする。
案2. コード片をツールに含める
コード片の管理場所。
素直に考えれば設定ファイル同様、.gnip/snippets/ みたいな専用フォルダを設けるのが第一案だ。
もちろん、フォルダパスは設定で変更可能にしても良い。
この場合、コード片のデバイス間同期をどうするかが気になるところだ。
とりあえずはユーザー(まあ自分以外のユーザーを想定する必要もあんまりないけど)が適当にハックすれば、.gnip/snippets/* を GitHub リポジトリとかの何らかのクラウドに上げて同期するようにはできる。
余裕があればツール側でサポート機能を作っても良い。
一方で、どうせ GitHub 上でコード片を管理したいなら、いっそ gnip 本体のコードと同じリポジトリで同時に管理しちゃう運用がいいかな、という気もしている。
一応ベースプロジェクトとして、gnip 本体コードのみのリポジトリは作っておく。
ユーザーはそれをフォークして、自分の登録したいコード片を専用フォルダ下に追加してコミットし、自分専用の gnip プロジェクトを育てていく。
gnip 本体にアップデートがあった時は、upstream ブランチを良い感じでマージとかすれば問題ない。
私は設定の変更履歴とかもコミットコメントで記録しておきたいタチなので、この作戦は良い感じに work しそうだと感じている。
今のところ最有力の案だ。
と、まあ
ここまでアイディアメモ。
scrapbox で箇条書きにしとけって感じだが、なんとなくナラティブにまとまりそうだったので記事にした。(まあまとまってないんだけど。)
これから諸々の既存ツールの仕様とかを調べてみる。
スニペット管理コマンドツール、普通に既にありそうな気もする。
車輪の再発明が好きなので、あえてちゃんと調べずにここまで思索した。
おわり。
AtCoder Beginners Selection を Ruby で解いた
AtCoder Beginners Selection(以下、ABS)
制限時間ガン無視で、エレガントさ重視で書いた。
ABC086A - Product
# frozen_string_literal: true a, b = gets.split(' ').map(&:to_i) product_is_even = a.even? || b.even? puts product_is_even ? 'Even' : 'Odd'
ABC081A - Placing Marbles
# frozen_string_literal: true puts gets.count('1')
ABC081B - Shift only
# frozen_string_literal: true _n = gets a = gets.split(' ').map(&:to_i) def divisible_count_by_2(num) quo, rem = num.divmod(2) rem.zero? ? divisible_count_by_2(quo) + 1 : 0 end count = a.map { |ai| divisible_count_by_2(ai) }.min puts count
提出結果2(パフォーマンス重視(のつもりだった))
※ 不必要なとこまで割り算をしないようにして、実行時間を短くするつもりだったが、無駄な工夫が災いしたのか実行時間はむしろ増大した。
# frozen_string_literal: true _n = gets a = gets.split(' ').map(&:to_i) class RemBy2Sequence include Enumerable def initialize(num) @last_quo = num end def each loop do @last_quo, rem = @last_quo.divmod(2) yield rem end end end count = a.reduce(Float::INFINITY) do |result, ai| RemBy2Sequence.new(ai) .each_with_index .lazy .take_while { |r, i| r.zero? && i < result } .count end puts count
# frozen_string_literal: true _n = gets a = gets.split(' ').map(&:to_i) count = a.map do |ai| ai.to_s(2).reverse.chars.take_while { |c| c == '0' }.count end.min puts count
ABC087B - Coins
# frozen_string_literal: true purse_coin500_count = gets.to_i purse_coin100_count = gets.to_i purse_coin50_count = gets.to_i total_amount = gets.to_i max_coin500_count = [purse_coin500_count, total_amount / 500].min pattern_count = (0..max_coin500_count).sum do |coin500_count| rest_amount_after500 = total_amount - 500 * coin500_count max_coin100_count = [purse_coin100_count, rest_amount_after500 / 100].min (0..max_coin100_count).count do |coin100_count| rest_amount = rest_amount_after500 - 100 * coin100_count coin50_count = rest_amount / 50 coin50_count <= purse_coin50_count end end puts pattern_count
ABC083B - Some Sums
# frozen_string_literal: true n, a, b = gets.split(' ').map(&:to_i) total = (1..n).find_all do |num| sum = num.to_s.chars.map(&:to_i).sum a <= sum && sum <= b end.sum puts total
ABC088B - Card Game for Two
# frozen_string_literal: true _n = gets.to_i a = gets.split(' ').map(&:to_i).sort_by { -1 * _1 } a << 0 if a.length.odd? alice_point, bob_point = a.each_slice(2).to_a.transpose.map(&:sum) puts alice_point - bob_point
ABC085B - Kagami Mochi
# frozen_string_literal: true n = gets.to_i a = Array.new(n) { gets.to_i } count = a.uniq.length puts count
ABC085C - Otoshidama
# frozen_string_literal: true bill_count, amount = gets.chomp.split(' ').map(&:to_i) amount /= 1000 # NOTE: treat amount in 1/1000 scale # NOTE: Persons drawn in bills at 2019: # 1,000 Yen : Hideyo Noguchi # 5,000 Yen : Ichiyo Higuchi # 10,000 Yen : Yukichi Fukuzawa State = Struct.new(:noguchi, :higuchi, :fukuzawa) do class << self def impossible new(-1, -1, -1) end end def bill_count noguchi + higuchi + fukuzawa end # DEBUG: # def amount # noguchi + higuchi * 5 + fukuzawa * 10 # end def to_s "#{fukuzawa} #{higuchi} #{noguchi}" end end # NOTE: Adjust bill_count while concerning states which amount is always right. max_noguchi_state = State.new(amount, 0, 0) if max_noguchi_state.bill_count < bill_count puts State.impossible exit end # let bill_count of a state near ASAP with exchanging noguchi to higuchi many_higuchi_state = lambda do |prev_state| exchange_count = [(prev_state.bill_count - bill_count) / 4, prev_state.noguchi / 5].min noguchi = prev_state.noguchi - exchange_count * 5 higuchi = prev_state.higuchi + exchange_count State.new(noguchi, higuchi, prev_state.fukuzawa) end.call(max_noguchi_state) # let bill_count of a state right with exchanging higuchi to fukuzawa goal_state = lambda do |prev_state| exchange_count = prev_state.bill_count - bill_count higuchi = prev_state.higuchi - exchange_count * 2 fukuzawa = prev_state.fukuzawa + exchange_count return State.impossible if higuchi.negative? State.new(prev_state.noguchi, higuchi, fukuzawa) end.call(many_higuchi_state) puts goal_state # puts goal_state.bill_count # puts goal_state.amount * 1000
ABC049C - 白昼夢
# frozen_string_literal: true class String def end_with?(*suffixes) suffixes.any? do |suf| len = suf.length suf == self[-len, len] end end end WORDS = %w[dream dreamer erase eraser].freeze str = gets.chomp def parsable?(str) return true if str.empty? first_word = WORDS.find { |word| str.end_with?(word) } return false if first_word.nil? parsable?(str[0, str.length - first_word.length]) end puts parsable?(str) ? 'YES' : 'NO'
提出結果2(同じことが Haskell ならできるのに〜)
※ 提出結果1がメモリ超過なのは末尾再帰最適化が Ruby には実装されてないため。Haskell ならそれが実装されているのでメモリを食わない。
import qualified Data.ByteString.Char8 as BS import Data.List import Data.Maybe main = do str <- BS.getLine putStrLn $ if solve str then "YES" else "NO" wordsForParse :: [BS.ByteString] wordsForParse = map BS.pack ["dream", "dreamer", "erase", "eraser"] parseTail :: BS.ByteString -> Maybe BS.ByteString parseTail str = find (`BS.isSuffixOf` str) wordsForParse solve :: BS.ByteString -> Bool solve str | str == BS.empty = True | otherwise = case parseTail str of Just w -> solve $ BS.take (BS.length str - BS.length w) str Nothing -> False
# frozen_string_literal: true class String def end_with?(*suffixes) suffixes.any? do |suf| len = suf.length suf == self[-len, len] end end end WORDS = %w[dream dreamer erase eraser].freeze str = gets.chomp def parsable?(str) rest = str loop do return true if rest.empty? first_word = WORDS.find { |word| rest.end_with?(word) } return false if first_word.nil? len = first_word.length rest.slice!(-len, len) end raise 'unexpected' end puts parsable?(str) ? 'YES' : 'NO'
# frozen_string_literal: true WORDS = %w[dream dreamer erase eraser].freeze str = gets.chomp def parsable?(str) index = str.length - 1 loop do return true if index.negative? parsed_word = WORDS.find do |word| len = word.length word == str[index - len + 1, len] end return false if parsed_word.nil? index -= parsed_word.length end raise 'unexpected' end puts parsable?(str) ? 'YES' : 'NO'
# frozen_string_literal: true str = gets.chomp def parsable?(str) rest = str loop do return true if rest.empty? word = first_word(rest) return false if word.empty? rest.slice!(0, word.length) end raise 'unexpected' end def first_word(str) if str.start_with?('dream') if str.start_with?('dreamer') && !str.start_with?('dreamera') 'dreamer' else 'dream' end elsif str.start_with?('erase') if str.start_with?('eraser') && !str.start_with?('erasera') 'eraser' else 'erase' end else '' end end puts parsable?(str) ? 'YES' : 'NO'
ABC086C - Traveling
# frozen_string_literal: true class SpaceVector attr_reader :x, :y def initialize(x, y) @x = x @y = y end def -(other) self.class.new(x - other.x, y - other.y) end def manhattan_length x.abs + y.abs end end class TimeSpaceVector attr_reader :time, :space def initialize(time, space) @time = time @space = space end def -(other) self.class.new(time - other.time, space - other.space) end end class Deer def can_move?(time_space) rest_time = time_space.time - time_space.space.manhattan_length rest_time >= 0 && rest_time.even? end end initial_point = TimeSpaceVector.new(0, SpaceVector.new(0, 0)) n = gets.chomp.to_i points = [initial_point] + Array.new(n) do t, x, y = gets.chomp.split(' ').map(&:to_i) TimeSpaceVector.new(t, SpaceVector.new(x, y)) end moves = points.each_cons(2).map { _2 - _1 } deer = Deer.new deer_can_move = moves.all? { |move| deer.can_move?(move) } puts deer_can_move ? 'Yes' : 'No'
実コードでモンキーパッチする時はちゃんと Refinements を使おうね。
おわり。
Vagrant で立てた CentOS7 に Ansible 入れようとした時のメモ
NG集
1
公式の案内に沿って
$ sudo yum install -y ansible
を行う。 -> "No package ansible available."
2
公式の続きをよく読むと、
RPMs for RHEL 7 and RHEL 8 are available from the Ansible Engine repository.
と書いてあり、repository の登録の仕方が書いてある。これが必要っぽい?先に言ってほしかった…。
というわけで案内に従い、
$ sudo subscription-manager repos --enable ansible-2.9-for-rhel-8-x86_64-rpms
を行う。 -> "subscription-manager: command not found"
3
$ sudo yum install -y subscription-manager
をしてからリベンジ。 -> "システムの証明書が破損しています。 再登録を行ってください。"
4
どうやら https://access.redhat.com/documentation/ja-jp/red_hat_subscription_management/1/html/rhsm/certs-update この案内に従って証明書とやらを更新しないといけないっぽい。めんどくさい。
成功集
1
社内で以下の記事を教わる: https://qiita.com/zaki-lknr/items/3ac4c7e105609a7f0bf9
これを参考に、
$ sudo yum install -y centos-release-ansible26 $ sudo yum install -y ansible
これでできた。
2
yum search ansible を行うと
centos-release-ansible-27.noarch : Ansible 2.7 packages from the CentOS ConfigManagement SIG repository centos-release-ansible-28.noarch : Ansible 2.8 packages from the CentOS ConfigManagement SIG repository centos-release-ansible-29.noarch : Ansible 2.9 packages from the CentOS ConfigManagement SIG repository centos-release-ansible26.noarch : Ansible 2.6 packages from the CentOS ConfigManagement SIG repository
と出る。見た感じ、ansible26 より新しいのがあるっぽい。(バージョン番号前にハイフンが入るようになっているのが罠。)というわけで、
$ sudo yum install -y centos-release-ansible-29 $ sudo yum install -y ansible
これで Final Answer。
3
pip 使うのが一番簡単って噂も社内で教わった。
おわり。
Vagrant 使おうとして調べたこととか
Vagrant 使わないとどうなるの?
例えば Ubuntu だとこんだけ初期設定が大変らしい。
こりゃ Vagrant 使うしかねえや。
Box はどれを選べばいいの?
公式ドキュメント(Install and Specify a Box | Vagrant - HashiCorp Learn)を見ると、
Warning: Namespaces do not guarantee canonical boxes, and anyone can publish boxes on Vagrant Cloud. HashiCorp's support team does not assist with third-party published boxes.
とのこと。
公式ドキュメントの他の箇所(Discovering Vagrant Boxes | Vagrant by HashiCorp)では、ユーザ名、ダウンロード数、最終更新日とかを調べるように書いてある。
The username of the user. If it's
bentoorubuntu, you can likely trust the box more than an anonymous user.
bento は信頼できるらしい。
IP 指定してアクセスしたいんだけど
private_network、forwarded_port, public_network のどれかのネットワークで指定する。
各ネットワークの違いは以下が詳しかった。
とりあえず外部に公開しないなら private_network で良い。
IP 何にすればええねん
一つの手として DHCP を指定することができる。
動的に変更されるのが嫌なら、何か固定値を指定するしかない。
private_network ならプライベートネットワーク IP(192.168.XXX.XXX とか)を指定するのが安全だろう。
既存のプライベートネットワーク IP とバッティングしたらどうすんねん
事前に使用済 IP を調べておいて回避するしかない。
LAN内で使用している IP を一覧取得するには、ping を飛ばしまくって確認するしかないっぽい。
まあ、思いついた IP に ping 飛ばしてみて、空いていたらそれを使えばいいだろう。
尚、自マシンが属するのと同じ 192.168.1.XXX を試しに指定してみたところ、以下のエラーが出て起動に失敗した。
The specified host network collides with a non-hostonly network! This will cause your specified IP to be inaccessible. Please change the IP or name of your host only network so that it no longer matches that of a bridged or non-hostonly network. Bridged Network Address: '192.168.1.0' Host-only Network 'en0: Wi-Fi (AirPort)': '192.168.1.0'
そんなこんなで大きな心配はなさそうだ。
IP の末尾を 1 にしたらなんか警告が出た
==> ansible: This is very often used by the router and can cause the ==> ansible: network to not work properly. If the network doesn't work ==> ansible: properly, try changing this IP.
とのこと。
複数マシンの一括設定ができるらしい
詳しくは公式ドキュメント参照(Multi-Machine | Vagrant by HashiCorp)。
共通の設定を一箇所にまとめつつ、個別の設定は個別に書く、みたいなことができる。
vagrant up で一括に起動したり、vagrant up <machine> で個別に起動したり等ができる。
Provisioning って何?なんか Ansible とかあるんだけど
ソフトのインストール作業とかも自動化するやつ。
公式ドキュメントにある Provisioning の "Ansible"(Ansible - Short Introduction | Vagrant by HashiCorp)は、対象仮想マシンを Ansible で初期化するやつだった。
(Ansible をインストールする初期化だと思ったのに、違った。)
そんなこんなでできた Vagrantfile
Ansible で遊ぶために以下の Vagrantfile を作った。
# -*- mode: ruby -*- # vi: set ft=ruby : <200b> Vagrant.configure("2") do |config| config.vm.box = "bento/centos-7" <200b> config.vm.define "ansible", primary: true do |ansible| ansible.vm.network "private_network", ip: "192.168.33.20" end (1..3).each do |n| config.vm.define "node#{n}" do |node| node.vm.network "private_network", ip: "192.168.33.1#{n}" end end end
おわり。
プログラミングにおける"フック"とは
フックの意味
フックという言葉には色々な意味がある。
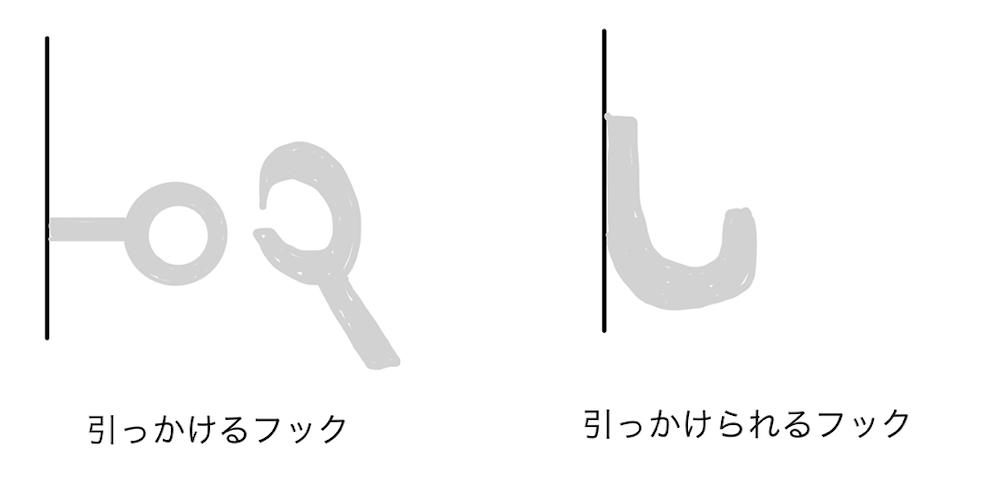
- 鉤。物を引っかける器具。
- 電話機で受話器を置く部分にあるボタン。フックスイッチを参照。
- 衣服の留めかぎ。ホック。こはぜ。
- 釣り針。
- 義手の手先金具、またはそれのついた義手。装飾義手(ハンドタイプ)ではない方の実用義手(フックタイプ)をいう。両腕義手の場合、複数形hooksとなる。
- BDSMで、使うフック。鼻フックが有名だが、他にも肛門や陰部に引っ掛けるプレイもある。
- フック (打撃) - ボクシングなどの攻撃の一種。引っ掛けるように横から打つ。
- ゴルフで右打者の打球が左に、また左打者の打球が右に大きく曲がること。
- フック (プログラミング) - コンピュータの処理を割り込ませる(引っかける)こと。
- つかみ - 芸能で、客を引きつけるためのしかけ。
- フック (音楽) - 覚え易い音楽の一節。
- フック - 航空機の機動の種類で、旋回中に急激に機首を旋回円の中心へ向けたまま機体の進行方向を変更しない機動。
- フックつき文字 - 文字の一部分を伸ばし曲げるようにして付け足した部分。
- フック符号 - 「?」の下の点を取ったような形のダイアクリティカルマーク。ベトナム語アルファベット(クオック・グー)で母音字の上に付ける。
共通するのは、「引っかける」という動作に関連したものということだ。
プログラミングにおけるフックの意味
プログラミングに関する部分だけ、もう一度引用する。
- フック (プログラミング) - コンピュータの処理を割り込ませる(引っかける)こと。
では、この意味のフックについて掘り下げてみよう。
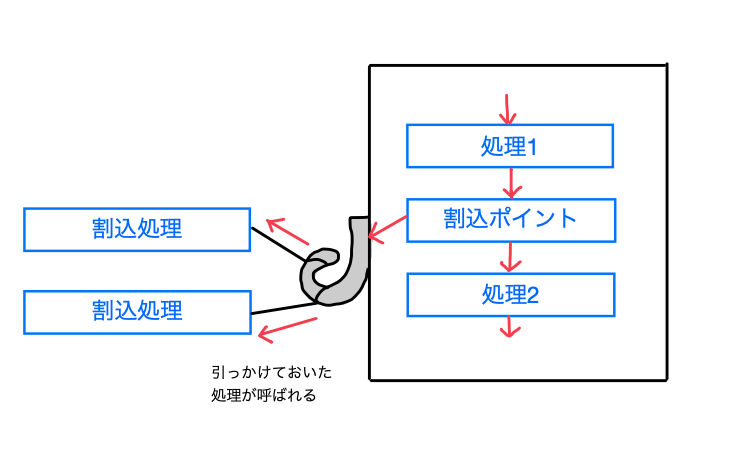
フック(Hook)は、プログラム中の特定の箇所に、利用者が独自の処理を追加できるようにする仕組みである。また、フックを利用して独自の処理を追加することを「フックする」という。
つまり、利用者が独自の処理を"引っかける"こと、または"引っかける"ことができる仕組みのことをフックというわけだ。
念の為、英語版の Wikipedia も確認してみよう。
In computer programming, the term hooking covers a range of techniques used to alter or augment the behaviour of an operating system, of applications, or of other software components by intercepting function calls or messages or events passed between software components.
関数呼出、メッセージング、イベントなどを"引っかける"ことを hooking (動詞:フックする)という。
Code that handles such intercepted function calls, events or messages is called a hook.
"引っかけられる"部分を hook (名詞:フック)というわけだ。
これは誤読だった。よく読むとこの文章は"引っかける"方を hook と呼んでいる。気がする。(どっち側も handle しているとは言えそうなので分かりづらい。しかし、後述の「イベントハンドラ」といった用語を考慮すると、"引っかける"方を指していると考えるのが自然な気がする。)
また、この記事の続きを読んでも "our hook function" 等の表現が見られ、どうも"引っかける"のに用いる処理の方を hook と呼んでいるように感じる。
しかし、他のいろいろな情報をあたってみると、"引っかけられる"方を hook と呼んでいる方が多い感じがする(例えば What is meant by the term "hook" in programming? - Stack Overflow とか)。
なのでこの記事では以降、独自の処理を"引っかけられる"方を hook とする解釈で進めていく。
フックのコード例
Wikipedia の例はシステムレベルの話が多い。もっと平凡なコードでフックを使ってみよう。
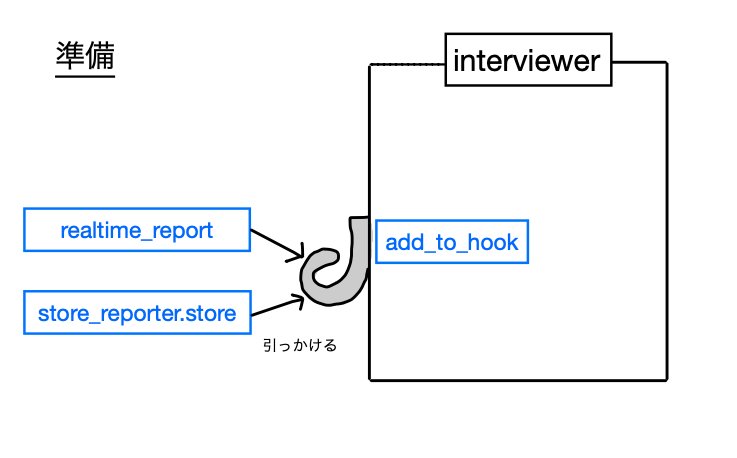
以下のような動きをするプログラムを Ruby で書く。
題材は、インタビューを取り扱うプログラムにしてみた。
プログラムが質問して、ユーザーが答える。それだけのやつ。
なるべく単純なコンソールアプリにしたいと思ったらこうなった。
そんなわけでコードがこれ。
# frozen_string_literal: true InterviewInfo = Struct.new(:question, :answer, keyword_init: true) class Interviewer def initialize @questions = %w[ 調子どうだ?カラダ? あなたは赤い部屋が好きですか? おまえは今まで食ったパンの枚数をおぼえているのか? てかLINEやってる? おいィ?お前らは今の言葉聞こえたか? 何いきなり話かけて来てるわけ? 質問文に対し質問文で答えるとテスト0点なの知ってたか? あなた…『覚悟して来てる人』……ですよね? 小便は済ませたか?神様にお祈りは?部屋の隅でガタガタふるえて命乞いする心の準備はOK? これはミラーシェード=サンのケジメ案件では? ] @hooked_funcs = [] end # フックに処理を引っかける def add_to_hook(func) @hooked_funcs << func end def interview @questions.shuffle.take(5).each do |question| puts question print '> ' answer = gets puts info = InterviewInfo.new(question: question, answer: answer) call_hooked_funcs(info) end end private # フックに引っ掛けられた処理を全部呼ぶ def call_hooked_funcs(info) @hooked_funcs.each { |f| f.call(info) } end end # フックに引っかける処理1 # 概要:インタビュー内容を逐次ログファイルに出力。 realtime_report = lambda do |info| File.open('realtime.log', 'a') do |file| file.puts "Q: #{info.question}" file.puts "A: #{info.answer}" end end # フックに引っかける処理2(store メソッドを引っかける) # 概要:インタビュー内容を store メソッドで蓄え、report メソッドで一気に出力。 class StoreReporter def initialize @interview_infoes = [] end def store(info) @interview_infoes << info end def report File.open('summary.log', 'a') do |file| file.puts '質問まとめ' @interview_infoes.each_with_index do |info, i| file.puts "#{i + 1}: #{info.question}" end file.puts '回答まとめ' @interview_infoes.each_with_index do |info, i| file.puts "#{i + 1}: #{info.answer}" end end end end store_reporter = StoreReporter.new # 準備:2つの処理をフックしておく interviewer = Interviewer.new interviewer.add_to_hook(realtime_report) interviewer.add_to_hook(store_reporter.method(:store)) # インタビューの実行 interviewer.interview # 処理2によって蓄えたインタビュー内容も出力 store_reporter.report
質問を行うオブジェクトは関数呼出をフックできるようになっており、実際に処理を 2 つフックしている。
ユーザーが 1 回質問に答える度に、フックした処理が 1 回ずつ呼ばれる形だ。
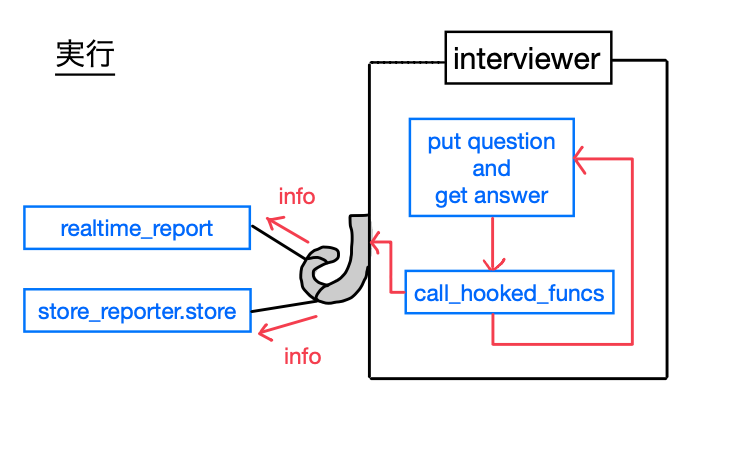
実行時のコンソールはこんな感じ。
【console】 小便は済ませたか?神様にお祈りは?部屋の隅でガタガタふるえて命乞いする心の準備はOK? > ミレニ……アム おいィ?お前らは今の言葉聞こえたか? > 俺のログには何もないな てかLINEやってる? > 笑 調子どうだ?カラダ? > 俺が楽天斎 質問文に対し質問文で答えるとテスト0点なの知ってたか? > マヌケ
出力結果はそれぞれ以下。
【realtime.log】 Q: 小便は済ませたか?神様にお祈りは?部屋の隅でガタガタふるえて命乞いする心の準備はOK? A: ミレニ……アム Q: おいィ?お前らは今の言葉聞こえたか? A: 俺のログには何もないな Q: てかLINEやってる? A: 笑 Q: 調子どうだ?カラダ? A: 俺が楽天斎 Q: 質問文に対し質問文で答えるとテスト0点なの知ってたか? A: マヌケ
【summary.log】 質問まとめ 1: 小便は済ませたか?神様にお祈りは?部屋の隅でガタガタふるえて命乞いする心の準備はOK? 2: おいィ?お前らは今の言葉聞こえたか? 3: てかLINEやってる? 4: 調子どうだ?カラダ? 5: 質問文に対し質問文で答えるとテスト0点なの知ってたか? 回答まとめ 1: ミレニ……アム 2: 俺のログには何もないな 3: 笑 4: 俺が楽天斎 5: マヌケ
無事、フックした2つの処理が呼ばれていることを確認できた。
話は少し脱線して、Ruby 固有のポイントに少し触れておく。
Ruby では 関数っぽいもの (例えばメソッドや、lambda 構文で生成されるやつ等)を変数に入れることができる。
そして、変数 f に 関数っぽいもの を入れた時、その 関数っぽいもの の呼び方は f(arg) ではなく、f.call(arg) となる。
なぜかというと、f に入っている 関数っぽいもの は、実際には 関数 ではなく、関数っぽい オブジェクト だからだ。
オブジェクト である以上は、なんらかのメソッドを呼ばない限り使うことはできない、というわけ。
全てがオブジェクトでできているというのは、 Ruby の大きな特徴の一つと言える。
フックとイベント駆動型プログラミングは似ている
コード例
上で書いたプログラムは、「イベント駆動型プログラミング」(日本版 wikipedia)の発想で書かれていると捉えることもできる。
試しに C# の event 構文を使ってプログラムを書き換えてみよう。
using System; using System.Collections.Generic; using System.IO; using System.Linq; namespace Interview { // ビルトインに足りない関数を追加している static class Extensions { private static readonly Random random = new Random(); public static IOrderedEnumerable<T> Shuffle<T>(this IEnumerable<T> list) { return list.OrderBy(item => random.Next()); } public static IEnumerable<(T, int)> WithIndex<T>(this IEnumerable<T> list) { return list.Select((item, index) => (item, index)); } } class InterviewFinishedEventArgs : EventArgs { public string Question { get; set; } public string Answer { get; set; } public InterviewFinishedEventArgs(string question, string answer) { Question = question; Answer = answer; } } delegate void InterviewFinishedEventHandler(InterviewFinishedEventArgs e); class Interviewer { private readonly string[] questions; public event InterviewFinishedEventHandler OnInterviewFinished; public Interviewer() { questions = new string[] { "調子どうだ?カラダ?", "あなたは赤い部屋が好きですか?", "おまえは今まで食ったパンの枚数をおぼえているのか?", "てかLINEやってる?", "おいィ?お前らは今の言葉聞こえたか?", "何いきなり話かけて来てるわけ?", "質問文に対し質問文で答えるとテスト0点なの知ってたか?", "あなた…『覚悟して来てる人』……ですよね?", "小便は済ませたか?神様にお祈りは?部屋の隅でガタガタふるえて命乞いする心の準備はOK?", "これはミラーシェード=サンのケジメ案件では?" }; } public void Interview() { foreach (var question in questions.Shuffle().Take(5)) { Console.WriteLine(question); Console.Write("> "); var answer = Console.ReadLine(); Console.WriteLine(); var info = new InterviewFinishedEventArgs(question, answer); OnInterviewFinished(info); } } } class StoreReporter { private readonly List<InterviewFinishedEventArgs> interviewInfoes = new List<InterviewFinishedEventArgs>(); public void StoreInterviewInfo(InterviewFinishedEventArgs info) { interviewInfoes.Add(info); } public void Report() { using (var w = new StreamWriter("summary.log", append: true)) { w.WriteLine("質問まとめ"); foreach (var (info, index) in interviewInfoes.WithIndex()) { w.WriteLine($"{index + 1}: {info.Question}"); } w.WriteLine("回答まとめ"); foreach (var (info, index) in interviewInfoes.WithIndex()) { w.WriteLine($"{index + 1}: {info.Answer}"); } } } } class MainClass { public static void Main(string[] args) { InterviewFinishedEventHandler realtimeReport = info => { using (var w = new StreamWriter("realtime.log", append: true)) { w.WriteLine($"Q: {info.Question}"); w.WriteLine($"A: {info.Answer}"); } }; var storeReporter = new StoreReporter(); var interviewer = new Interviewer(); interviewer.OnInterviewFinished += realtimeReport; interviewer.OnInterviewFinished += storeReporter.StoreInterviewInfo; interviewer.Interview(); storeReporter.Report(); } } }
実行結果は変わらないので省略。
C# 版のプログラムから event 構文に関係する部分を抜粋し、Ruby 版のプログラムから対応する部分を抜粋して並べてみる。
class InterviewFinishedEventArgs : EventArgs { public string Question { get; set; } public string Answer { get; set; } public InterviewFinishedEventArgs(string question, string answer) { Question = question; Answer = answer; } } delegate void InterviewFinishedEventHandler(InterviewFinishedEventArgs e); class Interviewer { public event InterviewFinishedEventHandler OnInterviewFinished; public void Interview() { OnInterviewFinished(info); } } class MainClass { public static void Main(string[] args) { interviewer.OnInterviewFinished += realtimeReport; interviewer.OnInterviewFinished += storeReporter.StoreInterviewInfo; } }
InterviewInfo = Struct.new(:question, :answer, keyword_init: true) class Interviewer def add_to_hook(func) @hooked_funcs << func end def interview call_hooked_funcs(info) end private def call_hooked_funcs(info) @hooked_funcs.each { |f| f.call(info) } end end interviewer.add_to_hook(realtime_report) interviewer.add_to_hook(store_reporter.method(:store))
こうしてみると、使っている言葉こそイベント駆動型プログラミング独特のものになっているが、やっていることはほとんど変わらないことが分かると思う。
詳しく見てみよう。
C# 版のプログラムで event キーワードを使って宣言している OnInterviewFinished。これがフックに相当する。
「InterviewFinished」というイベントが発生した時に呼び出すフック、というイメージでこういった命名をした。
event キーワードを使用したことで、フックへの処理の登録は interviewer.OnInterviewFinished += realtimeReport; という形で行えるようになっているし、登録された処理は OnInterviewFinished(info); の形で呼び出すことができるようになっている。
Ruby 版で書いた add_to_hook(func) のような処理や call_fooked_funcs(info) のような処理は必要ない。全部 event キーワードがよしなにやってくれている。
InterviewFinishedEventHandler というものを定義している行があるが、これはフックに登録できる関数の型みたいなものだ。
フックに登録できる関数は InterviewFinishedEventArgs 型の変数 e を受け取る、ということがここで読み取れる。
詳しく理解するためには、C# 特有の delegate 構文について知る必要があるだろう。
ここでは説明しないので ggrks。
InterviewFinishedEventArgs。これは Ruby 版で言うところの InterviewInfo に相当するクラスとなっている。
「InterviewFinished イベント」に関する情報を集めた変数(arguments)、というイメージの命名だ。
このクラスは EventArgs クラスを継承している。event キーワードを使う際にはこうしないといけない決まりになっている。
まあとにかく、C# の event キーワードを使ったこのプログラムは、Ruby で書いたフックプログラムと同じことをやっているということだ。
語彙の整理
上のプログラムでは EventHandler という言葉を使った。
これはイベント駆動型プログラミングの語彙だ。
イベントが発生した時に呼び出される処理のことを、「イベントハンドラ」(Event Handler)とよく言う。
フックから渡されるイベント情報を処理(ハンドリング)するイメージだ。
「イベントリスナ」(Event Listener)、「イベントレシーバ」(Event Reciever)等と言うこともある。
イベントハンドラをフックに引っ掛けること/フックから解除することについては、以下のような語彙を使う。
(Ruby 版のプログラムでは add_to_hook と書いた部分だ。)
- register/unregister
- add/remove
- subscribe/unsubscribe
イベントを発火させること(すなわち、フックされた関数にイベント情報を渡して呼び出すこと)については、以下のように語彙がたくさんある。
(Ruby 版のプログラムでは call_hooked_funcs と書いた部分。)
- raise
- trigger
- emit
- send
- invoke
- fire
- publish
語彙を置換してみる
フックを使った処理の説明を、イベント関係の言葉で置き換えてみよう。
「任意の処理を
フックに登録しておけば、
フックを持つ側のプログラムが
ある時点で
その処理を呼び出してくれる。」
↓
「任意のイベントハンドラに
イベントを購読させておけば、
イベントを持つ側のプログラムが
イベント発生時に
そのイベントハンドラを呼び出してくれる。」
というわけで、ふわっとした帰納的な説明ではあったが、フックとイベントは近い概念だということがなんとなく伝わったんじゃないかと思う。
"Web フック"とは
ここからが本番のつもりだったが、長くなっちゃったのでここで一旦区切ることにする。
続く。
作図ツール「draw.io」を使ってみたので紹介
概要
以下が draw.io 。
https://www.draw.io/
つまり、Web ブラウザ上で使える作図ツールということだ。
完全無料。すごい。
ファイルを開く/保存する
ファイルの参照/保存先として、Google Drive や Dropbox、GitHub 等のクラウドサービスが使える。
だが、一番簡単なのはローカルデバイスを指定することだ。
「ブラウザからどうやってローカルにファイルを保存するのか」と気になるかもしれないが、答えはすごく単純で、「保存」をする度にファイルのダウンロードが開始されるだけである。
なので毎回「名前をつけて保存」をしている感覚になる。「上書き保存」のような体験はできないので注意。(保存先がクラウドならできそう。試してない。)
なお、ファイルを開く際ももちろん、ローカルからアップロードすることになる。
ちなみに、保存しないままブラウザのタブを閉じようとすれば、ちゃんと確認ウィンドウが出てくれる。
ブラウザツールでありがちな「間違えて閉じてしまう」問題の心配もない。
ファイルの保存形式
drawio ファイルという独自の形式で保存される。中身は XML なようだが、肝心のコンテンツ部分は単一タグ内に暗号化された文字列がダーっと入っているだけだった。
その他、以下の形式に変換して保存(Export)することもできる。
- PNG, JPEG, SVG
- HTML
- XML
- 試してみたが、まんま drawio ファイルと同じだった。ちなみに Compressed のチェックを外すと、コンテンツ部分もそれっぽい XML できちんと表現されているのが観察できる。差分管理とかする場合はこの方がいいかも。
- URL
- ホスティングをしているのではなく、ファイルを暗号化した文字列を無理やり URL 内のパラメータに詰め込んでいるだけな気がする。
PNG, JPEG, SVG, PDF, HTML ファイルは、逆変換して開き直すこともできる(Import)。
もう少し確実な方法として、Export 時に「Include a copy of my diagram」にチェックを入れておくという方法がある。これをしておけば、drawio ファイルで無くとも変換無しで開く(Open)ことができる。
ちなみに、「Include a copy of my diagram」が具体的に何をやっているのか個人的に気になったので、チェックをオンにした SVG とオフにした SVG をそれぞれ Export して比較してみた。
その結果、どうやらチェックをオンにした場合は、非表示な領域に上手く drawio 形式の文字列を詰め込んでくれる、という感じのようだ。
drawio ファイルのままだと、例えば GitHub に上げた時などに、画像ファイルとして表示されなかったりして使い勝手が悪い。
かといって、単純な画像ファイルに Export してしまうと、再編集が困難になってしまう。
「Include a copy of my diagram」はこのジレンマを上手く解消してくれる。オススメ。
その他豆知識
PlantUML 変換
Arrange -> Insert -> Layout -> Advanced -> PlantUML
で、PlantUML データを図にして挿入することができる。
GitHub 連携
GitHub 上で draw.io の連携サービスを認可すると色々便利らしい。詳細は良く分からなかった。
プライベートリポジトリに関する権限を与えるのが怖いので、念のため試すのはやめた。
ツール
デスクトップツールが公式にある。
あとは非公式で VSCode のプラグインとかもあるっぽい。詳細は調べてない。
気になったリンク
- 【動画付き】 draw.io 使い方まとめ 〜エンジニアでなくても使えるTips集〜
- 今週 Qiita ランキング入りしてた。細かい機能紹介。
- 実践Drawio
- 細かい Tips 集。